Overtones
It it part and parcel of the science of music that when we play notes on instruments, we don't just hear those notes. Each note is actually made up out of lots of component notes, called overtones or harmonics.
Vibrations
When a musician sets a vibrating body in motion, a note is the end result. There are three basic forms of vibrating bodies: the string (e.g. the guitar), the column of air (e.g. the trumpet) or the solid block (e.g. the xylophone).
When something vibrates, it does so at a certain frequency. The frequency is defined by how many cycles occur per second, and is measured in what scientists and musicians alike call hertz (Hz). A frequency of 1 Hz is when something makes a complete cycle every second. If it occurs every other second, the frequency is 0.5 Hz. A common definition of the frequency range of the human ear is 20 Hz – 20 kHz, or pitches that oscillate between 20 and 20,000 times per second.
Subdivisions
However. The laws of physics also say that a vibrating body not only oscillates as a whole. It also does so in fractions: two halves, three thirds, four fourths, and so on until infinity. That's right: from the exact middle of the string, there are individual vibrational patterns that stretch all the way to both ends.
Since smaller vibrating bodies vibrate at higher frequencies, these partial vibrations yield higher-pitched notes. Taken together, all these notes create what we perceive as the fundamental note.
A note about word usage: one can always refer to the fundamental note, and its overtones, respectively. However, as we now shall find out, it is more intuitive and logical to refer to all notes as partials or harmonics, where the fundamental note is first among equals, or, less romantically, the first partial/harmonic.
The Overtone Series
We will now plot the first 16 harmonics using standard musical notation. In musical terms, the first subdivision (vibration in two halves) is exactly one octave above the fundamental note, and the second subdivision (three thirds) is an octave and a fifth above the fundamental. The first overtone has exactly twice the frequency of the fundamental, the second overtone three times the fundamental frequency. In other words, the frequency is in inverse proportion to the subdivision.
The notes derived from these partial vibrations can be arranged in a sequence, the overtone series. The following diagram illustrates the overtone series for the note 1C (corresponding to the lowest note on a cello, a major third below the low E on a guitar):
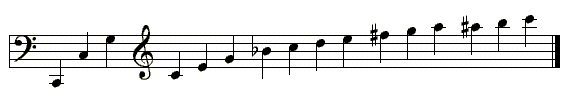
So, if you play 1C, you will actually hear all those other notes at the same time as well. And these are just the first 16 harmonics; the series continues indefinitely, but with progressively lower amplitude, and obviously, at 20 kHz, our ears no longer perceive any vibrations.
Note that some of the above notes are approximations. The seventh harmonic (B flat) is actually noticeably flatter than indicated, and the 11th harmonic (F sharp) is noticeably sharper. Music doesn't always add up!
Frequency Ratios
Since we know the frequency ratio between the first harmonic and all the others (1:n), we can also quite easily find out the ratios between other harmonics as well. If you put numbers under each note, 1 through 16, you will know exactly how to divide a string and what frequency that division will yield compared to the fundamental note.
If you locate all the C:s on the harmonic series, you will find that they are found in slots 1, 2, 4, 8 and 16. If you convert this to ratios, you will get 1:2, 2:4, 4:8 and 8:16. All these ratios can be simplified into 1:2. It is the same case with the G:s, which are found in slots 3, 6 and 12; 3:6 and 6:12 can also be simplified into 1:2.
Consequently, there are perfect fifths between harmonics 2 and 3, between 4 and 6, between 6 and 9 and between 8 and 12. These are all equivalent to the ratio 2:3.
So, if you want to find out the frequency ratio of a major sixth, find the interval on the harmonic series. I can find two occurrences: G (harmonic #3)/E (harmonic #5) and G (harmonic #6)/E (harmonic #10). The ratio 6:10 can be simplified into 3:5.
The simplest frequency ratios yield the most consonant intervals: unison (1:1), octave (1:2), fifth (2:3) and fourth (3:4). This is why these intervals are referred to as the perfect intervals. The more complicated frequency ratios yield thirds, sixths, seconds and sevenths, which are the intervals that appear in two basic qualities: major and minor. This will be elaborated upon in the essay on interval theory.
Difference Tones
A difference tone is a psychoacoustic phenomenon where a third note is perceived when playing a two-note interval. The frequency of the difference tone is derived by subtracting that of the lower note from that of the higher.
Beating
Difference tones are the reason behind the oscillation, or "beating", evinced by out-of-tune instruments, or people playing or singing not quite in unison. The frequency is simply low enough that the individual oscillations can be perceived. Even a miniscule difference in frequency—for instance that between 400 and 401 Hz (0.25%!)—will create a wobbling beating with the frequency of one cycle per second (401 Hz−400 Hz = 1 Hz).
The Doubling Effect
Difference tones are also the underlying reason why some musical intervals are more powerful than others. The difference between notes in consonant intervals creates a fortifying doubling of the root (or the octave below), which I will now prove by basic arithmetic:
The octave has a frequency ratio of 1:2. If the lower note is at 100 Hz, the higher note will be at 200 Hz. The difference tone will be at 200 Hz − 100 Hz = 100 Hz, which is a perceived doubling of the lower note.
The perfect fifth, ratio 2:3, also has a consonant difference tone. If the lower note is at 200 Hz, the perfect fifth will be at 300 Hz. 300 Hz − 200 Hz = 100 Hz. The difference tone will be exactly one octave below the lower note.
Simple Is Best
As previously stated in the chapter on interval theory, the unison (harmonic ratio 1:1), octave (1:2), fifth (2:3) and fourth (3:4) are the four simplest intervals, collectively referred to as the perfect intervals partly due to theirs being the most basic harmonic ratios, and the fact that those intervals remain perfect when inverted.
One of them, however, is not like the others. Which one, and why?
It turns out that the fourth has very interesting properties when you consider difference tones. Since the harmonic ratio is 3:4, a note at 300 Hz and one at 400 Hz will find themselves at the interval of a perfect fourth. Subtract 300 from 400 to get the frequency of the difference tone. This is where the interesting stuff starts to happen: 100 Hz is two octaves below 400 Hz (1:2:4)—the difference tone will be two octaves below the higher note!
This confirms two things: 1) that the fourth is an inverted fifth, thereby interchangeable, thereby more properly described as an interval class. And 2) many theorists state that the fourth is actually a dissonant interval, chiefly because our ears are attuned to tertian harmony, which expects unisons, thirds and fifths. Remember your chord theory: fourths are the result of a suspension or at least the addition of a non-chordal note.
As you move on towards smaller and smaller intervals, the difference tone becomes lower, until—as described above—it is less of a tone and more of an oscillation.
Finding Overtones
When I first heard about the concept of overtones, I thought: "what a weird theory, that's got to be impossible to prove!" I mean, how can all those notes (see the music example above) sound at the same time and not sound like a cacophony?
It turns out there are several ways to "prove" that there are overtones:
Sinus Tones
Without overtones, all musical notes would sound like the noises the ear doctor plays in headphones when he checks your hearing. These notes are pure notes, pure frequencies, without overtones. They are technically known as sinus tones since they are naught but a simple sine wave.
Even vs. Uneven Harmonics
Harmonics make up all the difference between what we perceive as musical sounds and what we think is noise. All sounds are vibrations! The difference is how the amplitude (science speak for volume) of the harmonics is distributed. If you tap your fingernail against a glass or a cup, you are rewarded with a musical "ping". Take the same glass and throw it on a concrete floor for some decidedly unmusical sounds. It's all about harmonics.
Isolating Harmonics
On a guitar, harmonics can be isolated very easily and heard in their true form. All you have to do is keep the open string from ringing. You do this by touching it very lightly before you strike it. You can stop the string just about anywhere, and there is likely to be some form of harmonic, but it is by far more efficient if you do so over a harmonic nodal point.
It is relatively easy to locate these points, since the the laws of acoustics are with us. Since different pitches on a guitar are produced by stopping the strings at various places on the neck, the fretwire can be used as a roadmap to harmonics.
The 12th fret is one octave above the open string, and the laws of physics therefore dictate that it has to be placed exactly midway between the bridge and nut. Touch the string lightly over the wire of the 12th fret and strike the note. The second harmonic rings out.
The third harmonic—an octave and a pure fifth above the open string—is found over the 19th fret. But since the third harmonic is derived from a division of the string into thirds, there is also a second place where you can isolate the third harmonic. This nodal point is halfway between the 19th fret and the nut: the 7th fret. (Note how smoothly everything comes together: if you stop the string behind the 19th fret, you get a note exactly one octave above that behind the 7th fret. Why? Because the 19th fret is exactly halfway between the 7th fret and the bridge!)
This goes on and on up until the nodal points are so tightly packed together close to the nut and bridge that they cannot be isolated.
Resonance
Muting is important when playing electric guitar, especially when you use lots of distortion. One of the reasons is that unwanted string sounds are easily amplified by volume and compression. Another reason is sympathetic resonance. Perhaps you've heard it in your rehearsal room: when you hit certain notes on the guitar or bass, the snare drum resonates along with your instrument. It works exactly the same on a guitar. If you strike the top E string and mute it quickly, the bottom E string and very likely the A string as well will start vibrating at the common frequency. Used properly on an acoustic guitar, you can make a decent simulation of a room reverb.