Chord Theory

A chord is the simultaneous or sequential sounding of three or more different notes, or perhaps more properly pitch classes.

Perception

The musical brain is more or less subconsciously conditioned to perceive chords even when they aren't explicitly sounded. Partly this is because as per the definition above, what sounds like a melody might very well spell out chords or parts of chords. Part of it is due to the compound nature of the individual note (which consists of overtones). It should be mentioned that although the common definition of a chord is at least three pitches, many times it is quite enough with just two to imply a chord.

Stacking Thirds

With 12 available notes, out of which any three (or four or more) can be combined into chords, one might get the impression that the potential combinations are nigh on infinite. There is indeed a multitude of possible combinations of three individual pitch classes. It's just that far from all of them are perceived as valid chords.

The human ear and brain tends to gravitate towards tertian chords—chords that are built up out of thirds—possibly because of the influence of the overtones that underpin everything in music. Tertian harmony has ruled Western music for centuries. It is only comparatively recently that composers have explored alternate ways to build chords, such as secundal and quartal harmony, but those are beyond of the scope of this article.

In order to make a tertian chord, take a note and stack a third on top of it. Then stack another third on top of that. Since interval theory gives that 3 + 3 = 5, the span of the chord will be a fifth. Since there are several kinds of thirds (major, minor, diminished etc.), there are many ways to construct subtly different chords. It is also possible to continue adding notes, which we will see shortly.

The notes that make up a chord are called chord members and take on names from at which intervals the upper notes fall in relation to the lowest note (in root position—see inversions below).

• The root note is the most important note of the chord, the harmonic anchor if you will.
• The third is the second most important note. It determines whether the chord is a major or minor chord.
• The fifth adds fullness to the chord.
• Further notes are added as needed in order to add coloration to the chord. As the stacking of thirds is (mostly) consistent, these extension notes are the seventh, ninth, eleventh and thirteenth.

I like saying that the root gives the chord its identity and the third and fifth (and any extension notes) its personality.

Triads

The simplest, and by far most common chords are called triads, which is Greek for three-note chords.

Basic Triads

The two most important triads are the major and minor triads. In addition to the root note, both have a perfect fifth. The difference between the chords is the third. If it is major, it is a major triad, if it is a minor third, it is a minor chord:

Altered Triads

There are also four possible altered triads, meaning that the fifth has been lowered or raised, for a slightly dissonant sound. There are two altered minor triads and two altered major triads, one of each of whom are more prominent in music theory: the diminished triad and the augmented triad:

As you can see, the diminished triad has a minor third and a diminished fifth. The augmented triad has a major third and an augmented fifth.

Triad Interval Structure

• Major and minor triads span a total of seven semitones.
• The major triad is built from 4 + 3 semitones, since it consists of a major third and a minor third.
• The minor triad is built from 3 + 4 semitones; the proportions are reversed.
• The diminished triad is made up of six semitones (3 + 3), or two minor thirds.
• The augmented triad is made up of eight semitones (4 + 4), or two major thirds. The augmented triad is symmetrical, because there are then four semitones between the augmented 5th and the octave. This means that the intervals remain the same upon inversion (more on that later).

The other two possible altered triads are the minor augmented fifth triad, and the major diminished fifth triad. These are not that common, mostly due to the fact that the former has an interval structure that is enharmonically equivalent to a first-inversion major triad (see below). The latter is close to secundal harmony due to the diminished third (2 semitones) between the upper two chord members. However, both may be used as the basis for extended chords of four or more notes.

Four-note Chords

For obscure historical reasons, triads are the only chords that use the Greek number. As we add more notes, we revert to the decidedly less romantic four-note chords, five-note chords, and so on.

As already hinted, the reason to tack extra notes onto an otherwise fully featured chord is to achieve some form of coloration effect. This effect might be purely decorative, or it might be a deliberate attempt to introduce dissonance, which creates tension that can then be resolved by moving to less dissonant harmonies.

Seventh Chords

A seventh chord is a triad with the addition of a seventh. There are two basic triads and you can add either a minor or a major seventh. This gives us four basic seventh chords:

The first example, the C major triad with the appended B♭, is commonly referred to as a dominant seventh chord. It has the simplest chord symbol of the four basic seventh chords, implying that it has some kind of special status. Indeed it has. Chances are when someone refers to a seventh chord, they actually mean this kind of seventh chord. We will explore exactly why in a little bit.

Diminished Seventh

Diminished seventh chords are very special. They consist of a diminished triad to which you add—not a minor but a diminished seventh.

Dim7 chords have all sorts of interesting properties. First and foremost, they are perfectly symmetrical. There are three semitones between each chord member, and when you stack yet another minor third on top of the diminished seventh, you will find yourself back at the octave! This means that any of the notes in the chord can be regarded as the root.

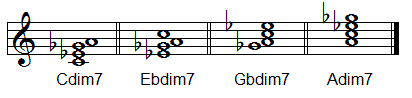
A careful scrutiny of the above music example will reveal that I have taken the liberty of making some enharmonic substitutions in the interest of clarity. B𝄫 sounds just like A on an even-tempered instrument.

Sixth Chords

A sixth chord is a major or minor triad with the addition of a major sixth:

Sixth chords are technically not tertian chords, as there is a major second between the fifth and the sixth of the above example. The illustration also underlines that a sixth chord always contains a major sixth, even if it's a minor sixth chord. This will also be explained below.

Sixth and Seventh

It is a valid question why sixth chords always contain a major sixth (no matter if they're minor or major), and that the most common seventh chord is a major chord with a minor seventh. This is because they trace their origins to classical harmony. Typically, such notes are added to chords in order to create tension that is then resolved. As such, they tend not to appear freely, but only on certain chords within a particular key.

The sixth is commonly appended to a subdominant chord (IV; an F major triad in C major), and the seventh to a dominant chord (V; a G major triad in C major). Tension is maintained throughout the sequence, and then the resolution appears upon the movement from the V7 to the tonic (I) chord:

(Never mind the voice leading, as this is not a treatise on harmony.) The D in the F major sixth chord is slightly dissonant, but it also anticipates the D that is the fifth of the G seventh chord. There is also a dissonance between the B and F (third and seventh) of the G chord that wants to resolve by shrinking stepwise to C and E—the root and third of the C chord.

If we instead switch the key to the parallel minor and write out a similar I-IV6-V7-I sequence:

The iv6 chord, here an F minor sixth chord, still contains that D, because D is common to both C major and C minor. Likewise, the dominant seventh chord on G contains a F—another common note across both keys. This example also illustrates the principle behind the harmonic minor scale: note that the naturally occurring B♭ has been raised to B♮ creating a major dominant seventh chord with a stronger pull towards resolution in C minor (or, for that matter, C major).

Extended and Altered Chords

Extended Chords

Chords with five or more notes are spread out over more than an octave and are therefore known as extended chords. All extended chords continue the principle of stacking thirds on top of the root:

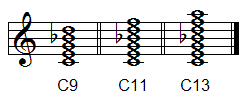
• A ninth chord is a seventh chord with an added ninth.
• An eleventh chord is a seventh chord with an added ninth and eleventh.
• A thirteenth chord is a seventh chord with an added ninth, eleventh and 13th. It also looks like it's going to require your entire forearm to play.

When you get to a 13 chord, all seven scale degrees are present in the chord, so no further stacking of thirds is possible. (Or, to quote Nigel Tufnel from Spinal Tap, "by the time you get to 13 the song's over anyway".) There are no 15th chords, because a 15 is a double octave.

Altered Chords

Altered chords are chords where the fifth and/or any of the extension notes (9th, 11th or 13th) has been chromatically altered. These chords will be discussed in a bit more detail in the essay on chord symbols.

Voicing and Inversion

Voicing

It is important to understand that the definition of a chord is three or more pitch classes rather than three or more notes. This means that it is perfectly acceptable to have certain notes doubled. Moreover, the notes do not necessarily need to appear in the exact same order in which they are found in the scale.

A chord voicing is how you space the chord on one or more musical instruments or voices. The voicing determines if any or all of the chord members are doubled, in which register (or octave) they are situated, and which chord member is the bass note.

All the following chords are perfectly valid voicings of a C major triad:

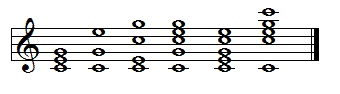
The first and fifth voicings are in close position, i.e. there are as few musical gaps between notes as physically possible. The others are in open position, i.e. with more separation between the notes. Notice that all voicings have C as the root note. These chords are all in root position, which we will discuss shortly when talking about inversions.

The first two voicings contain only barest minimum of notes, the chord members C, E and G. The third through sixth voicings have one or more doubled notes. Doubling reinforces certain aspects of the chord, likewise does the placement of the most prominent top note:

• Doubling the root note reinforces the tonal identity of the chord.
• Doubling the third reinforces the minor/major character.
• Doubling the fifth adds fullness to the chord.

Inversion

If the root note is the bass note, i.e. it is the lowest note in the chord and all other notes are played higher up, the chord is said to be in root position. If any other note is the bass note, the chord is considered to be inverted.

Triads have two possible inversions, since there are two notes other than the root:

Four-note chords have three, since there is also a seventh:

Chord Relations

Relative Major/Minor

Relative chords are chords that are situated three semitones apart and have two notes in common. This always falls so that the major chord is a minor third above the minor chord:

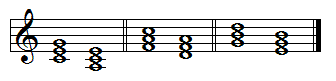
As you can see, the C major triad is relative with A minor (C and E in common), F with Dm (F and A in common) and G with Em (G and B in common).

In C minor, it looks like this:

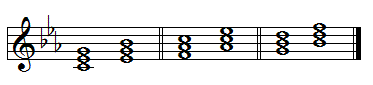
The C minor triad is related to E♭ major (E♭ and G in common). The F minor triad is related to the A♭ major triad (A♭ and C in common). Lastly, the G minor triad shares two notes with the B♭ chord—B♭ and D.

Thus, the upper two notes of the minor chord are common with the lower two notes of the major chord.

As there is a natural kinship between relative chords, they can frequently substitute for each other within a harmonic context without increasing the tension unduly. This concept can be extended to scales and even keys: C major contains the same notes as A minor, and so on.

Counter-parallel/Leading-note Exchange Chords

The sharp-eyed reader might already have made the connection that there are actually two ways that chords can have two notes in common. If we instead focus on the upper two notes of a major triad, we see that the chord has those notes in common with the minor chord a major third above it:

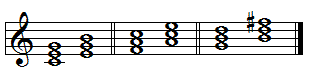
The C major chord has E and G in common with the E minor chord. The F major chord has A and C in common with the A minor chord. The G chord has B and D in common with the B minor triad, even though it does require a bit of cheating with a sharp.

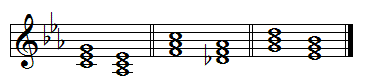
In C minor above, the C minor triad has C and E♭ in common with the A♭ major triad. The F minor chord has F and A♭ in common with the D♭ chord (notice the slight cheat here as well!). The G minor chord has G and B♭ in common with the E♭ chord.

Theorists have not been able to reach a consensus on what to actually call this kind of chord relation. Since they are kind of relative to one another, but "in the other direction", one name that has surfaced is "counter-relative". They have also been described variously as "opposite" or even leading note exchange chords. This since they only differ by a leading note: shift down the root of a C major triad to create an inverted E minor triad.